좌표계

2D 좌표계

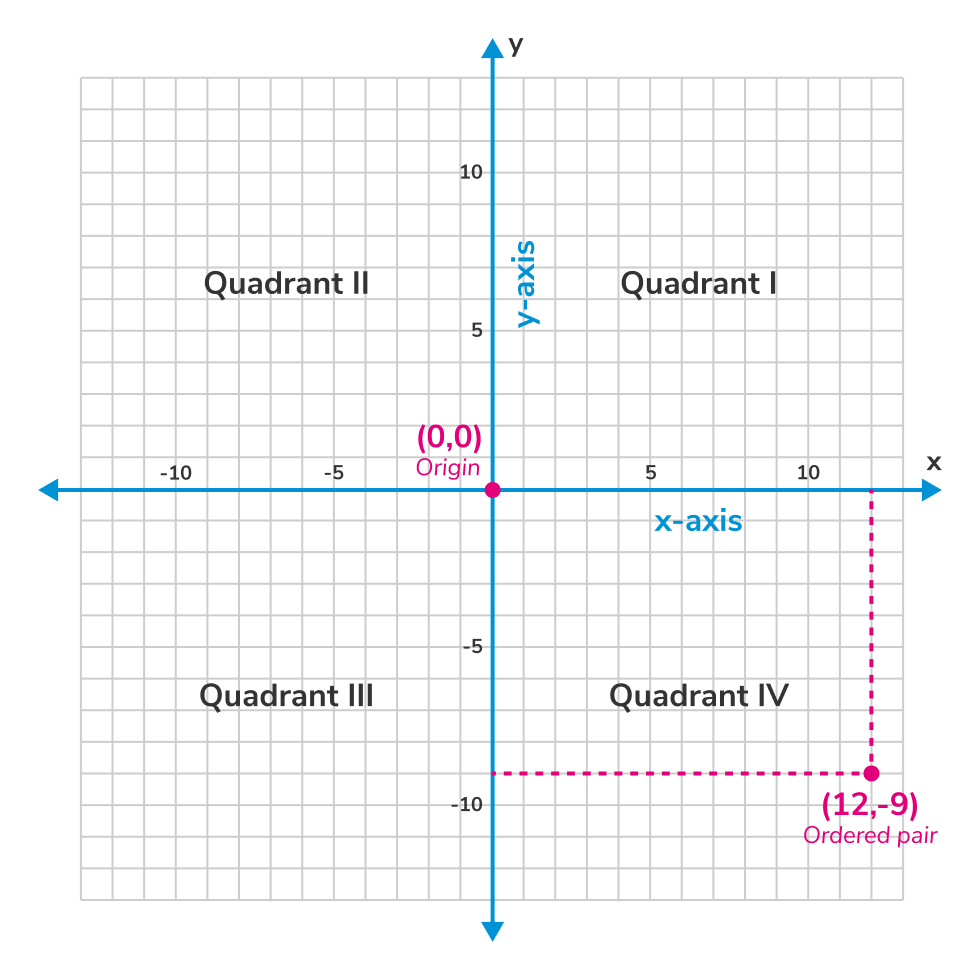
좌표계는 물체의 위치를 특정한 하나의 점으로, 유일하게 가리키기 위한 체계이다. 원점에서
직각으로 교차하는 x축과 y축으로 이루어진 좌표계를 직교좌표계라고 한다.(데카르트 좌표계라고 부르기도 한다.)

x축과 y축에 의해 네 개로 분할된 평면을 사분면이라고 하고, 오른쪽 위에서부터 반시계 방향으로 1사분면, 2사분면, 3사분면, 3사분면으로 구분한다. 직교좌표계를 사용하면 2차원 평면상의 위치를 유일하게 지정할 수 있으므로 2D 게임의 모든 장면에서 쓰인다.

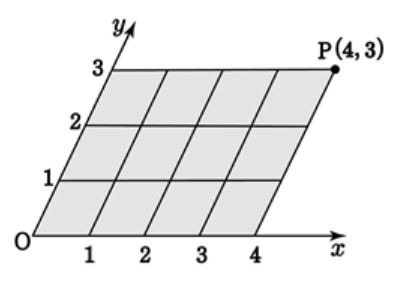
축이 직각으로 교차하지 않는 사교좌표계라는 것도 존재한다.

3D 좌표계

x축, y축 두 개의 직각으로 교차하는 축을 사용하면 2D 평면상의 위치를 지정할 수 있는데, 여기서 축을 하나 늘려, x축, y축에 z축을 추가해서 세 개의 직각으로 교차하는 축을 사용하면 (x, y, z)라는 세 개의 값으로 3D 공간 내의 특정 위치를 지정할 수 있다. 3D 직교좌표계는 유니티에서 게임 씬 내 GameObject 위치를 나타내는 데 쓰인다.

왼손 좌표계와 오른손 좌표계

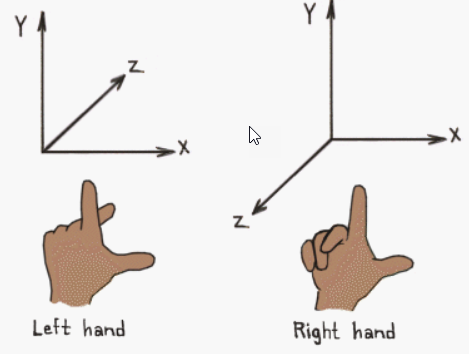
유니티, Direct X, 언리얼 엔진은 2D 평면을 나타내는 직교좌표계에서 채용한 오른쪽으로 x축, 위쪽으로 y축인 위치 관계의 좌표계를 기준으로, 원점에서 안쪽을 향해 깊이로서 z축이 증가하는 왼손 좌표계를 채택한다.
OpenGL, WebGL에서는 2D 평면에서 앞쪽을 향해 z축이 늘어나는 다시 말해, 앞쪽으로 올수록 z 값이 증가하는 오른손 좌표계를 채택한다.

왼손 좌표계와 오른손 좌표계는 z축을 기준으로 거울에 비추듯 바꾸면 서로 변환할 수 있지만, 어디까지나 서로 다른데, 이 겹치지 않는 그런 관계를 손대칭성 또는 카일랄성이 있다고 한다.

왼손 좌표계, 오른쪽 좌표계라는 이름이 붙은 이유는 왼손과 오른쪽의 엄지를 x축, 검지를 y축, 중지를 z축이라고 했을 때 z축의 방향에서 유래한다.

로컬 좌표계, 월드 좌표계, 스크린 좌표계

로컬 좌표계: 오브젝트 기준 시점의 좌표이다.

월드 좌표계: 유니티의 가상 공간의 기준 좌표이다.
스크린 좌표계: 화면 왼쪽 아래 구석을 원점으로, 화면 해상도에 따른 픽셀 위치를 단위로 하는 2D 직교좌표계이다.

예를 들어 화면 해상도가 1920 X 1080이면 왼쪽 하단 구석은 (0,0) 우측 상단 구석은 (1920,1080) 이 된다.

뷰포트 좌표: 스크린 좌표계를 정규화한 값

2D 극좌표계

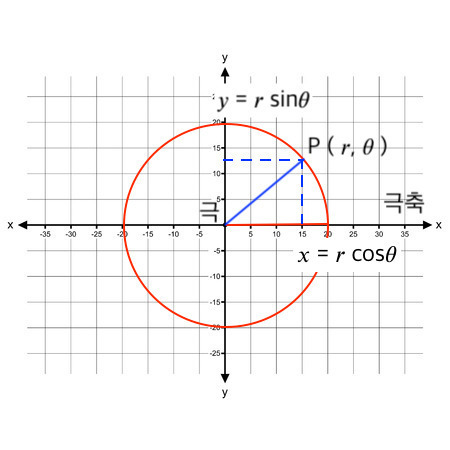
2D 직교좌표계에 원점이 있듯 2D 극좌표계에도 세계의 중심에 극이라 불리는 기준점이 있다. 
또한, 직교좌표계에서 원점에서 가로 방향으로 x축이 뻗어가듯 극에서는 극축이라 불리는 반직선이 뻗어나온다.

극좌표계에서 평면상의 점 P의 위치를 결정하는 것은 극축과 P를 연결하는 직선 r의 길이와, 극축과 r이 이루는 각도 θ이다. 이 두 값으로 P의 극좌표는 (r, θ)로 지정된다.

2D 극좌표를 나타내는 그림은 단위원 그림과 거의 같은데, 다른점은 단위원의 반지름은 1인 반면, 극좌표계에서 원의 반지름 r은 실제 점 P의 위치에 따라 변한다는 것이다. 반지름 길이가 다를 뿐이기 때문에 삼각함수의 원리는 그대로 성립한다. 다시 말해 2D 극좌표계 (r, θ)는 2D 직교좌표(r, cosθ, sinθ)와 같다. 거꾸로 2D 직교좌표(x, y)를 극좌표로 표현하면, 피타고라스의 정리와 삼각함수를 이용해 다음과 같이 나타난다. 

(sqrt(x^2+y^2), atan2(y, x))

게임에서 극좌표는 평면상에서 원의 원주 위를 이동시킬 경우, 사용할 수 있다. 또, 화면 중심으로부터의 거리에 따라 화면에 특정 이미지 처리를 가하고자 할 때, 직교좌표계인 스크린 좌표계에서 극좌표로 변환해주면 처리가 쉽다.

3D 극좌표계 = 구면 좌표계

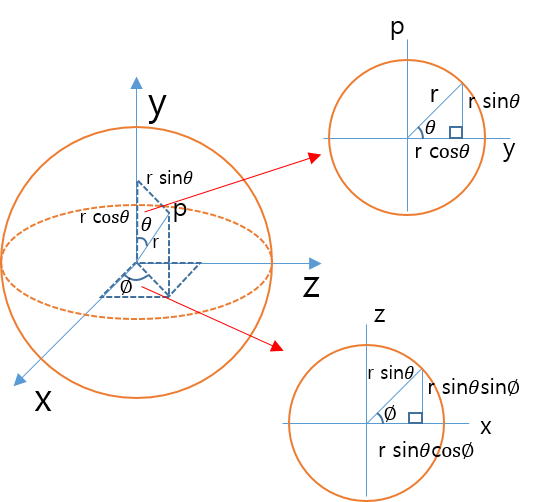
직교좌표계에서 z축을 추가해 3D 직교좌표계를 정의할 수 있는 것처럼, 극좌표에서도 축을 하나 더 추가하면 3D 극좌표계를 정의할 수 있다. 2D 극좌표에서는 반지름의 길이와 극축과의 각도로 좌표를 지정했지만, 3D 극좌표계에서는 또 하나의 축과 이루는 각도를 추가하여, 세 개의 값으로 좌표를 정의한다. 이 3D 극좌표계를 구면좌표계라고도 부른다.

구면좌표계의 좌표는 관례적으로, 반지름의 길이 r과 2가지 축의 양의 방향으로부터의 각도 θ와 Φ(파이)의 3가지 수치의 조합(r, θ, Φ)으로 표현한다.
구면좌표계 자체는 2D 극좌표계에 축을 하나 더했을뿐이므로, 2D 극좌표계처럼 삼각함수를 사용해서 3D 직교좌표계와 서로 변환할 수 있다. 다시 말해, 왼쪽좌표계의 직교좌표축에서는 구면좌표 P(r, θ, Φ)를 직교좌표로 표현하면 다음과 같다.

(r sinθ cosΦ, r cosθ, r sinθ sinΦ)

 

게임에서는 특정 캐릭터의 로컬 좌표공간 내에서 원형 궤도를 도는 위성처럼 움직이는 물체를 표현하거나, 캐릭터의 후방 상공 떠서 일정한 거리로 캐릭터를 추적해 화면 중심에 계속 비추는 3인칭 시점 게임의 카메라에 사용한다.